Critical notes of Quantum Mechanics: Momentum Operators

Abstract

In this note, we examine critically some basic features of momentum operators, both in the case of simple spatial context and in the case of spacetime. The natural time for the domain H of the momentum operator The Laurent Schwartz space S_n endowed with its own semimetric topology and with the Dirac inner product

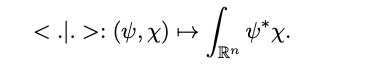
We emphasize that the right topology to consider is the standard Schwartz topology, not the topology induced by the above Dirac inner product which needs to provide probability issues and not continuity properties. The above choice for the space H satisfy at once some fundamental requirements of the theory:
0. all the functions of the space H are both smooth and square integrable;
1. the operator P reveals indeed a linear endomorphism everywhere defined upon
H;
2. the operator is continuous with respect to the Schwartz topology;
3. the operator P is uniquely extensible to the entire space of tempered distributions
S_n′ and this extension is continuous with respect to the standard topology of such distribution space.
4. The above unique extension shows the so-called de Broglie waves as natural eigenvectors, although those de Broglie waves are not square integrable.

The above third and fourth points induce us to consider that extension as the standard right choice for the momentum operator, not only because that extension contains in- side the previous operator defined on the Schwartz function space, but because - even more stringently - the space of temperate distributions allow us to define rigorously the fundamental concept of continuous quantum state basis and the concepts of Dirac orthogonality and Dirac normalizability for such type of bases. It happens, by the way, that some de Broglie families of quantum waves are indeed quantum basis of the space S_n′ and reveal Dirac orthogonal and Dirac normalizable.